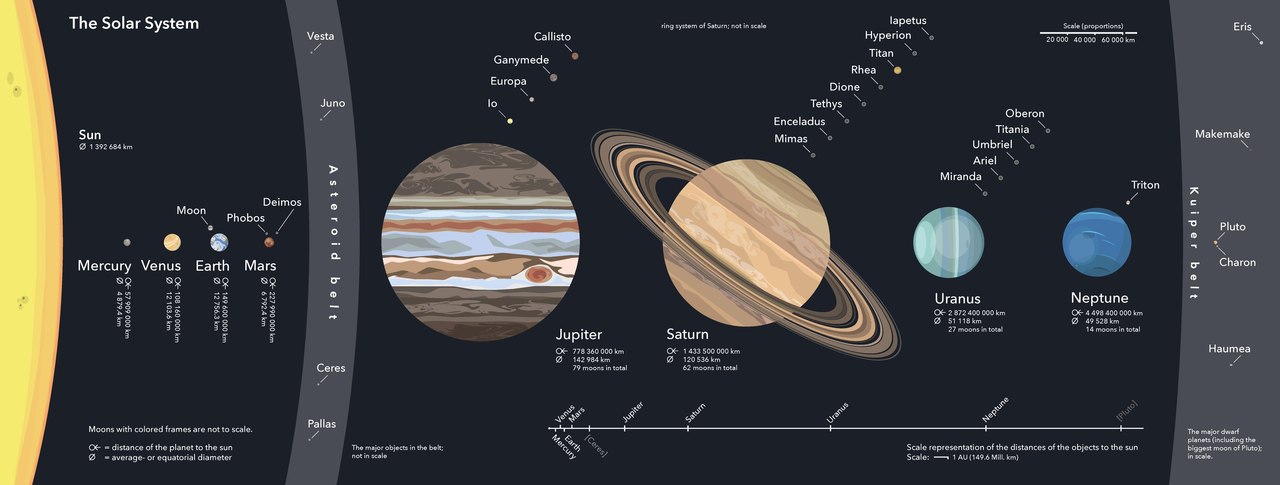
Solar System: Interesting Facts about Planets and the Sun

Solar System is a group of celestial bodies which revolves around the star named, the Sun. It is called a system because all planets move around the star in a more or less predictable fashion. Our planet, our home, Earth is also part of the solar system. Apart from planets, the solar system also consists dwarf planets, minor planets, satellites and comets.

The solar system is a single star system. Nicolaus Copernicus formulated the heliocentric solar system. Heliocentric means centered around the Sun. In 1533, Copernicus presented his work stating that the Sun is the center of the Universe and not the Earth. Now we know that Copernicus was right in saying that the Earth revolves around the Sun — but we still do not know whether the Universe has a center, and if it has then whether the Sun is that center!

Important Points about the Solar System

Solar System is composed of the following:

• 1 Star (Sun)
• 8 planets (Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus and Neptune)
• 5 dwarf planets (Ceres, Pluto, Eris, Haumea and Makemake)
• 796,354 minor planets
• 575 natural satellites (like the Moon of Earth)
• 4,143 comets

How old is the Solar System? Well, our Solar System was formed 4.568 billion years ago.

Where is the Solar System located? Out Solar System is located in the Orion Arm of the Milky Way Galaxy.

The Sun lies between 25,000 and 28,000 light-years from the center of the Milky Way.

The solar system is tilted at about 60° angle to the Milky Way plane.

You already know that all the planets revolve around the Sun. But did you know that the solar system as a whole also keeps moving? Well, yes! it does! The solar system moves at about 220 km/s along with the Milky Way.

The solar system completes one revolution around the Milky Way in every 225–250 million years. This is called Solar System’s galactic year.

The Sun is is our nearest star. After sun, our closest stars are Proxima Centauri (4.25 light years away) and Alpha Centauri (4.37 light years away). Sun light takes 8 minutes and 20 seconds to reach Earth.

The Sun has 99.86% of the total mass of the entire solar system.

Jupiter is the largest and Mercury is the smallest planet in the Solar System.

The world no longer considered Pluto as a planet. Pluto has now been classified as a dwarf planet.

Venus and Uranus are the only planets that rotate in retrograde direction. That is, the Sun of these planets rises in the west and sets in the east.

An asteroid belt exists between Mars and Jupiter. Based on this asteroid belt, the planets have been divided into two parts:

• Inner planets: The planets that exist between Sun and the asteroid belt. These are Mercury, Venus, Earth and Mars
• Outer planets: The planets that exist beyond the asteroid belt. These planets are Jupiter, Saturn, Uranus and Neptune

The inner planets are rocky and much smaller than the outer planets.

The outer planets are gaseous (also known as gas giants) and much bigger than the inner planets.

Most of the solar system is still unknown to us. Although, Pluto is not considered a planet now, but most people may think that the solar system ends at Pluto. This is not true! The solar system extends to the all the region within the influence of the Sun’s gravity. Some estimates put this influence field up to two light years.

Jupiter has the largest ocean in the solar system. This ocean of liquid hydrogen is about 40,000 kilometers (25,000 miles) deep.

Many people think that Mercury could be the hottest planet because its nearest to the Sun. But in truth, Venus is the hottest planet with surface temperatures over 400 °C (752 °F). This higher temperature is because of the greenhouse effect in the atmosphere of Venus.

Mercury and Venus are the only planets in the solar system that do not have any natural satellites (or moons, so to speak).

Inner planets have none or few natural satellites. Whereas the outer planets, or gas giants, posses large number of satellites. Jupiter has 79, Saturn has 82, Uranus has 27 and Neptune has 14 natural satellites.

Our planet Earth is mostly composed of elements like Iron, Oxygen, Silicon, Magnesium, Sulfur, Nickel, Calcium, Sodium, and Aluminum. But rest of the solar system is predominantly made up of Hydrogen and Helium gases.